Frequent Itemset Mining

While building a recommendation system, we need a good sense of users’ preferences, which can be approximated by their previous interactions with our system. This approximation goes for a toss if we ever encounter a new user about whom we know little or nothing. This is a very relevant problem in Recommender Systems literature and commonly known as the cold start problem [2]. To tackle this issue, we may recommend popular items which other users have interacted with. Another way to recommend items to users is by recommending items that are frequently associated with the current item the user is interacting with. We can find the sets of items that occur together in our user histories and create frequent itemsets.

This is a fundamental problem in data mining and is known as the Frequent Itemset Mining problem, and the main algorithm that is used to solve this problem is called the A-priori Algorithm [1].

Motivation

We create sets of items that appear together to leverage this information for the marketplace to sell more relevant products. For example, the sale of beer may see a significant spike during the FIFA World Cup. The marketplace may also have the information that chips and beer go hand in hand; that is, people who come in to buy beer also buy chips. The store can then leverage this information by placing the chips that give greater profit margins closer to the beers that are selling the most.

Terminology

• Transaction - Cart contents of a single user constitutes as a single transaction.
• Items - Set of all the products that the marketplace is selling.
• Itemset - A set if items.
• Support ($s$) - For a given itemset $I$, the proportion of transactions that contain $I$.
• Frequent Itemset - The itemset $I$ that appear appear more that the minimum Support Threshold transactions.

For example -

The sets of items that appear more that 40% of the time in our transactions constitute as the frequent itemsets.

Naive Algorithm

We can set up our naive algorithm that find the frequent itemsets of increasing size iteratively. We can assume that we have our transaction dataset which contains one transaction per line with items separated by comma.

1. Frequent itemsets of size 1

The first step will be to find the frequent itemset of size one. This can be done by creating a hashmap of all the items in our transactions and keep the count of all the items. We can do this by a single pass through our data. The items that appear more than the given minimum support constitute as the frequent itemsets.

freq_items = defaultdict(int)
with open('data.txt', 'r') as f:
    for line in f:
	    line = line.split(',')
	    for item in line:
		    freq_items[item] += 1

freq_items = {item: count for item, count in freq_items.items() if count/num_transactions >= min_support}

For a given set of transactions this takes around $O(n)$ memory where $n$ is the number of items in the data.

2. Frequent Itemsets of size 2

The second step of finding the frequent itemsets of size 2 can be performed in the same way. We can again create a hashmap that stores the count of all possible pairs appearing in the data. This can also be done by scanning through the data once.

freq_pairs = defaultdict(int)
with open('data.txt', 'r') as f:
	for line in f:
    line = line.split(',')
    for i, item_1 in enumerate(line):
        for j, item_2 in enumerate(line[i+1:]):
            freq_pairs[frozenset([item_1, item_2])] += 1

This will require a memory of around $O(n^2)$. Which proves to be bottleneck for datasets containing large number of items.

For e.g. The Enron Email Dataset [3] which contains around $n = 28000$ items (tokens). Assuming that we require 16 bits to represent one item. We’ll need at least 30GB of main memory available to store the counts of each possible pair. This memory requirement explodes even further when we calculate frequent itemsets of size 3 and above.

To tackle this issue, we use a fundamental data mining algorithm available in the literature - A-priori algorithm.

A-priori Algorithm

We saw in the previous section how the memory requirements explodes as we keep on increasing the length of the itemsets. For a given iteration can we leverage the results from the previous iterations?

Key Idea : Monotonicity
If the set of Items, $I$, appear at least $s$ times in the data, so does every subset of $I$.
If an Item $i$ does not appear $s$ times itself, no set containing $i$ can appear $s$ times.

We can use this information to eliminate a lot of itemset pairs. As for each potential pair, each item should be frequent for the pair to be frequent.

1. Finding the Frequent Itemsets of size 1.

This step is similar to the naive algorithm, we create a hashmap which stores the count of each items which appears at least $s$ times.

For the Enron Dataset with $min_support = 0.05$, the number of frequent items is equal to $282$ out of $28099$ possibilities

2. Generating Candidates for the Frequent Itemset Pairs.

In this step we include all those pairs which are candidates to be the frequent pairs based on the monotonicity property.

freq_pair_candidates = {}
with open("data.txt", 'r') as f:
    for line in f:
        line = line.split(',')
        for i, item_1 in enumerate(line):
            for j, item_2 in enumerate(line[i+1:]):
                if item_1 not in freq_items or item_2 not in freq_items:
                    continue
                freq_pair_candidates[frozenset([item_1, item_2])] = 0

In this step we’ve eliminated all the pairs which can not be frequent, hence greatly reducing our memory requirements. We would have needed around 30GB to store all the pairs in the memory. Using the A-priori rule, we have reduced the search space to only $40000$ candidate pairs (out of possible 789M). \(\begin{align*} Memory\ Reduction &= (1 - len(candidate\_pairs)/(n(n-1)/2))*100\\ &= 99.99\% \end{align*}\)

3. Find the Frequent Itemsets for size 2

To find the frequent itemsets of size 2, we scan through the dataset once again. For each occurrence of a candidate pair we increase its count by one.

with open("data.txt", "r") as f:
    for line in tqdm(f):
        line = line.split()
        for i, item_1 in enumerate(line):
            for j, item_2 in enumerate(line[i+1:]):
                if frozenset([item_1, item_2]) not in freq_pair_candidates:
                    continue
                freq_pair_candidates[frozenset([item_1, item_2])] += 1

freq_pairs = {pairs:count for pairs, count in freq_pair_candidates.items() if count/num_transactions >= min_support}

4. Finding Frequent Itemset of size 3 and above

We can generalize the creation of frequent itemsets of size $k$ using the following procedure. For each iteration $k$, we can create two k-sets (sets of size k) -

• $C_k$ = candidate k-sets = those sets that might be frequent sets (support $\geq$ min_support ) based on the information from the (k-1)-sets.
• $L_k$ - the set of truly frequent k-sets.

This can be depicted by the following figure -

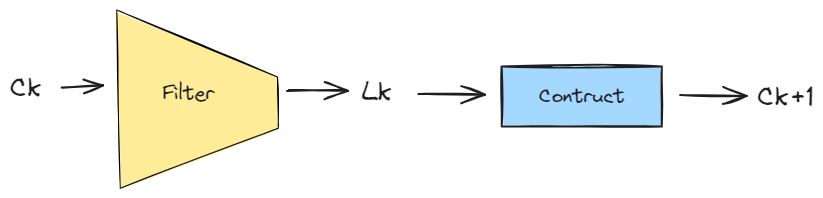
Frequent Itemset Generation Using Candidates

For the first iteration (k=1), the entire set of items are candidates, starting from the next iteration we apply the monotonicity property to construct the candidates accordingly.

References

1. Agrawal, R. and Srikant, R. (1994) Fast Algorithms for Mining Association Rules in Large Databases. Proceedings of the 20th International Conference on Very Large Data Bases, Santiago de Chile, 12-15 September 1994, 487-499.
2. Rashid, Al & Albert, Istvan & Cosley, Dan & Lam, Shyong & McNee, Sean & Konstan, Joseph & Riedl, John. (2002). Getting to Know You: Learning New User Preferences in Recommender Systems. International Conference on Intelligent User Interfaces, Proceedings IUI. 10.1145/502716.502737.
3. Klimt, B., Yang, Y. (2004). The Enron Corpus: A New Dataset for Email Classification Research. In: Boulicaut, JF., Esposito, F., Giannotti, F., Pedreschi, D. (eds) Machine Learning: ECML 2004. ECML 2004. Lecture Notes in Computer Science(), vol 3201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-30115-8_22.

Tweet Share