How Low-Rank Adaptation (LoRA) Changes the Geometry of Self-Attention

- 8 mins
LoRA Attention Machine Learning Deep Learning Transformers

How Low-Rank Adaptation (LoRA) Changes the Geometry of Self-Attention

Introduction

Low-Rank Adaptation (LoRA) is typically presented as a parameter-efficient alternative to full fine-tuning, motivated by reducing memory and compute costs. While the low-rank formulation explains how LoRA reduces the number of trainable parameters, it does not explain why LoRA is particularly effective in attention-based models.

This post analyzes LoRA from a geometric perspective, focusing on how low-rank updates reshape the attention mechanism itself. We combine mathematical intuition with a minimal PyTorch implementation to empirically demonstrate how LoRA alters attention scores and distributions while keeping the backbone frozen.

Self-Attention as a Geometric Operation

Given an input sequence $X \in \mathbb{R}^{n \times d}$, self-attention computes:

\[Q = X W_Q, \quad K = X W_K, \quad V = X W_V\]

The attention output is:

\[\text{Attention}(X) = \text{softmax}\left(\frac{Q K^\top}{\sqrt{d}}\right) V\]

Each query vector $q_i$ defines a direction in embedding space. Attention weights depend on the angular alignment between $q_i$ and all key vectors $k_j$. From this view, self-attention performs a context-dependent projection of values onto a subspace defined by query–key similarity.

A Minimal Self-Attention Implementation

To ground this discussion, we start with a minimal single-head self-attention module. The goal is not efficiency or completeness, but explicit access to intermediate tensors for analysis.

class TinySelfAttention(nn.Module):
    def __init__(self, d_model: int):
        super().__init__()
        self.d = d_model
        self.q_proj = nn.Linear(d_model, d_model, bias=False)
        self.k_proj = nn.Linear(d_model, d_model, bias=False)
        self.v_proj = nn.Linear(d_model, d_model, bias=False)

    def forward(self, x):
        Q = self.q_proj(x)
        K = self.k_proj(x)
        V = self.v_proj(x)

        scores = (Q @ K.transpose(-2, -1)) / math.sqrt(self.d)
        attn = F.softmax(scores, dim=-1)
        out = attn @ V
        return out, Q, K, scores, attn

This implementation makes the geometry explicit: queries and keys interact via dot products, producing a score matrix that determines how information flows across tokens.

LoRA in Attention Layer

LoRA modifies a projection matrix $W \in \mathbb{R}^{d \times d}$ as:

\[W' = W + BA\]

where:

The update $\Delta W = BA$ has rank at most $r$, constraining learning to a low-dimensional subspace.

Minimal LoRA Implementation

We implement LoRA by wrapping an existing linear layer and adding a trainable low-rank residual branch. The base weights remain frozen.

class LoRALinear(nn.Module):
    def __init__(self, base: nn.Linear, r: int = 4, alpha: float = 8.0):
        super().__init__()
        self.base = base
        for p in self.base.parameters():
            p.requires_grad = False

        self.A = nn.Parameter(torch.randn(r, base.in_features) * 0.01)
        self.B = nn.Parameter(torch.zeros(base.out_features, r))
        self.scale = alpha / r

    def forward(self, x):
        base_out = self.base(x)
        lora_out = (x @ self.A.t()) @ self.B.t()
        return base_out + self.scale * lora_out

Initializing $B=0$ ensures that the LoRA branch starts as a no-op, making the effect of adaptation easy to isolate.

Injecting LoRA into Self-Attention

We now apply LoRA only to the query projection:

attn = TinySelfAttention(d_model=64)
attn.q_proj = LoRALinear(attn.q_proj, r=4)

Keys and values remain unchanged. Any change in attention behavior must therefore arise from query reorientation alone.

Effect on Attention Scores

Recall that attention scores are computed as:

\[S = \frac{Q K^\top}{\sqrt{d}}\]

With LoRA applied:

\[Q' = Q + \Delta Q\]

This introduces an additive term:

\[S' = \frac{(Q + \Delta Q) K^\top}{\sqrt{d}}\]

Importantly, LoRA does not rewrite the score matrix arbitrarily; it introduces a structured, low-rank perturbation.

Empirical Evidence: How LoRA Alters Attention Geometry

We now analyze the effect of LoRA through a sequence of visualizations. All plots are generated by keeping the input sequence fixed and training only the LoRA parameters on the query projection, while freezing the backbone.

The target during training is to make query token 0 attend strongly to key token 5.

Attention Distribution Before LoRA

Figure: Attention map BEFORE LoRA training 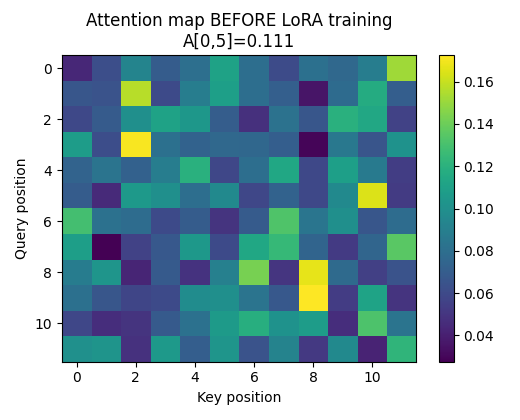Attention Before LoRA

Key observations:

This is expected behavior for an unadapted model with random initialization or generic pre-training.

Attention Distribution After LoRA Training

Figure: Attention map AFTER LoRA training 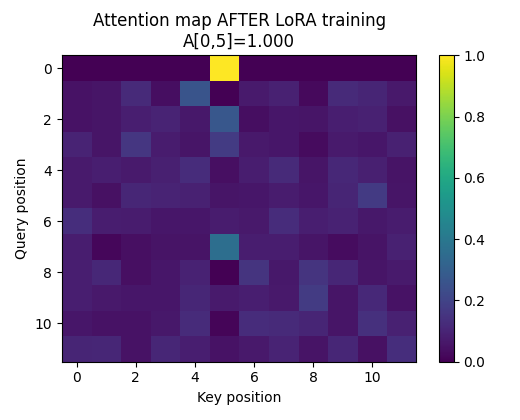Attention After LoRA Interpretation: LoRA introduces a targeted reallocation of attention mass. Crucially:

This demonstrates that LoRA enables localized control over attention routing rather than wholesale retraining.

Score Matrix Before LoRA (Pre-Softmax Geometry)

Figure: Score matrix BEFORE LoRA — $QK^\top / \sqrt{d}$ 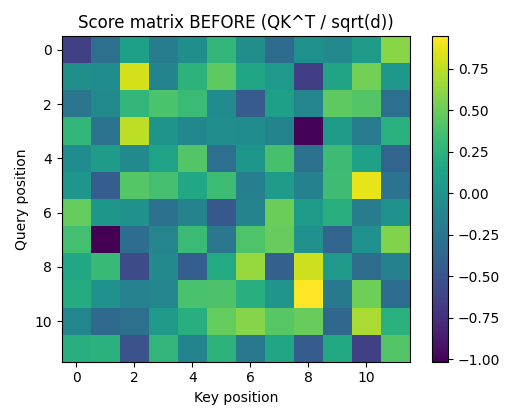Scores Before LoRA This matrix represents the raw geometric interaction between queries and keys before softmax.

Observations:

Score Matrix After LoRA

Figure: Score matrix AFTER LoRA — $Q’K^\top / \sqrt{d}$ 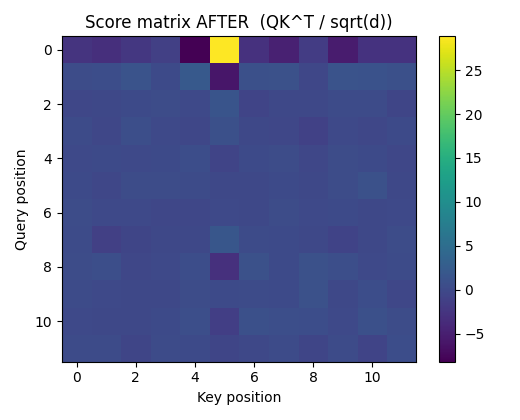Scores After LoRA

Key changes:

Interpretation:

LoRA modifies the score matrix via the term: \(\Delta S = \frac{\Delta Q K^\top}{\sqrt{d}}\) Since keys are frozen, this confirms that query rotation alone is sufficient to reshape attention geometry.

Query Rotation: Directional Change

Figure: Per-token cosine similarity $\cos(Q_{\text{before}}, Q_{\text{after}})$ 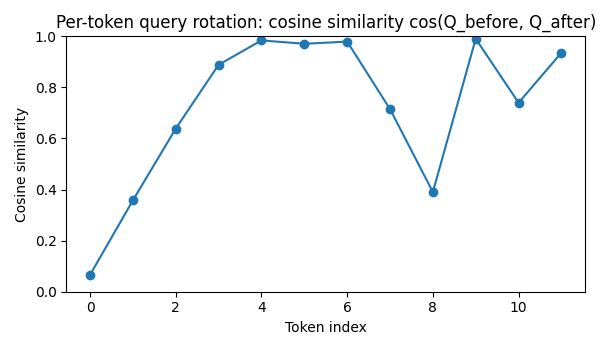Query Cosine Similarity This plot measures directional change in query vectors.

Observations:

Interpretation:

This supports the geometric view of LoRA as subspace reparameterization.

Query Update Magnitude

Figure: Per-token $|\Delta Q|$ magnitude after LoRA training 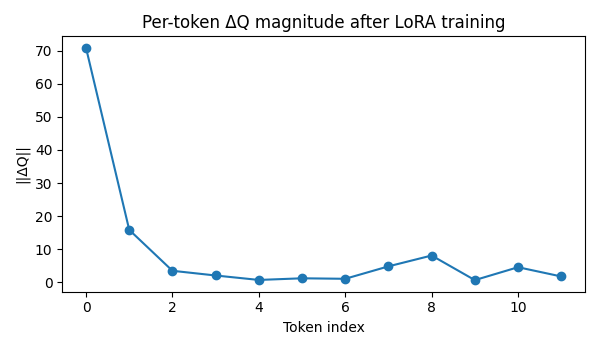Query Update Magnitude

Observations:

Interpretation:

Although LoRA parameters are shared across tokens, the model learns to apply uneven geometric influence, concentrating adaptation where it matters. This explains why LoRA is both:

Why LoRA Works Well on Queries

Modifying queries affects:

Keys serve as anchors; excessive modification destabilizes similarity structure. LoRA’s low-rank constraint ensures stable, localized adaptation.

Conclusion

LoRA is effective not merely because it is parameter efficient, but because it aligns naturally with the geometry of self-attention. By restricting updates to a low-rank subspace, LoRA performs controlled rotations of query directions, leading to targeted changes in attention without disrupting the backbone.

Understanding LoRA at this geometric level provides practical guidance on: - where to apply it - how to choose rank - and why it outperforms naive fine-tuning in large attention-based models.

References

  1. Hu et al., LoRA: Low-Rank Adaptation of Large Language Models, ICLR 2021
  2. Vaswani et al., Attention Is All You Need, NeurIPS 2017
  3. He et al., Towards a Unified View of Parameter-Efficient Transfer Learning, ICLR 2022
  4. Dettmers et al., QLoRA, NeurIPS 2023

Related Posts