Parameter Efficient Fine Tuning (PEFT) – Adapting Large Models at Scale
- 4 minsParameter Efficient Fine Tuning (PEFT) – Adapting Large Models at Scale
Introduction
Large-scale neural networks, particularly transformer-based architectures, have become the dominant paradigm for representation learning in language, vision, and multimodal systems. While pre-training on large corpora enables strong general-purpose representations, downstream adaptation remains challenging due to the computational and memory cost of full fine tuning.
Parameter Efficient Fine Tuning (PEFT) methods address this challenge by enabling task adaptation through training a small subset of parameters while keeping the majority of the pre-trained model frozen. This approach significantly reduces training cost while preserving the representational power of the base model.
This post presents a detailed technical discussion of PEFT methods, their mathematical formulation, and architectural implications. 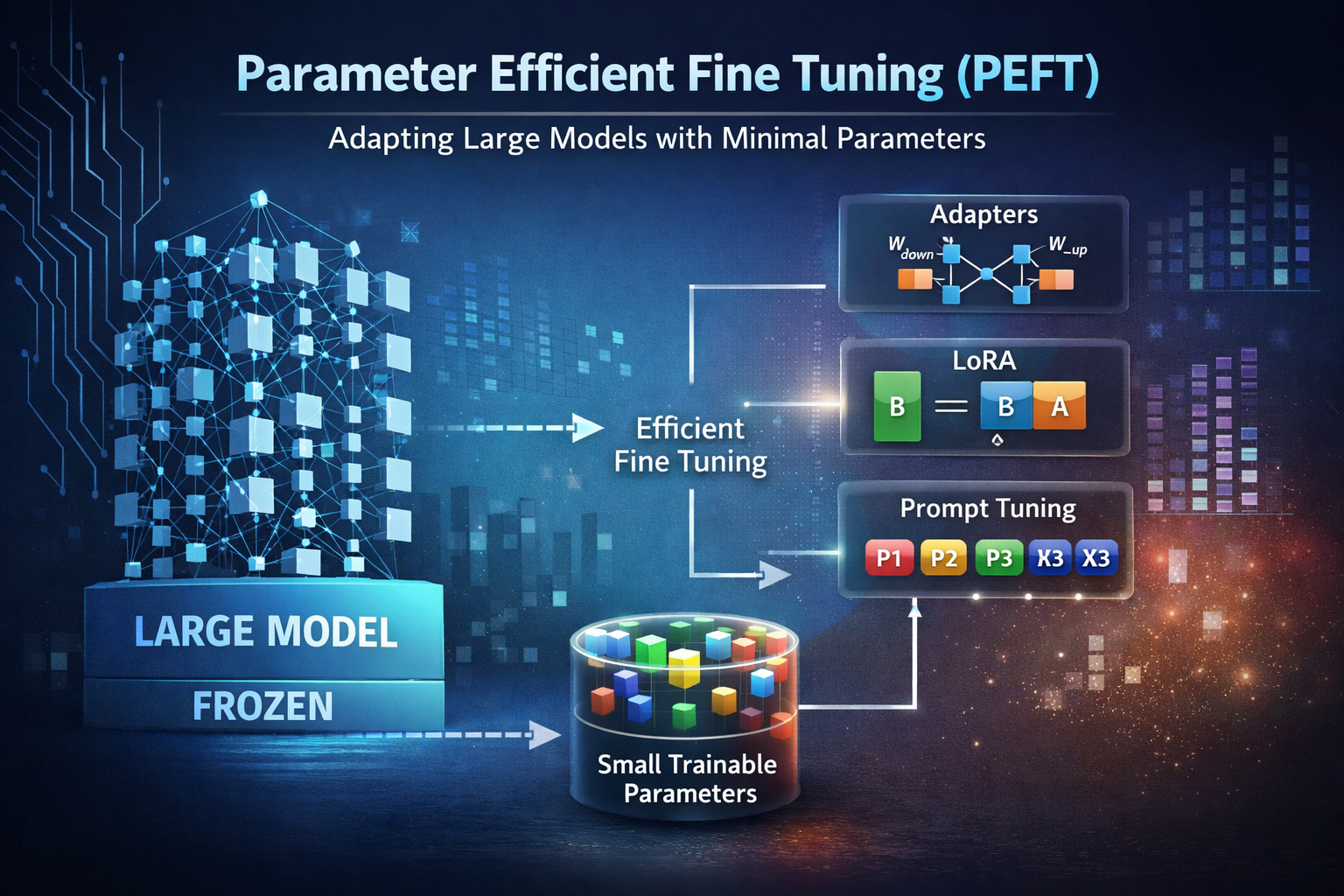
Limitations of Full Fine Tuning
Let a pre-trained model be parameterized by $\theta \in \mathbb{R}^N$, where $N$ is typically in the order of billions.
Full fine tuning requires:
- Gradient computation and storage for all parameters
- Optimizer state memory proportional to model size
- Large-scale distributed training infrastructure
More importantly, full fine tuning often results in:
- Redundant parameter updates
- Overfitting on smaller downstream datasets
- Catastrophic forgetting of pre-trained knowledge
Empirical studies show that downstream tasks frequently require only localized modifications to pre-trained representations rather than global re-optimization.
Formal Definition of PEFT
PEFT decomposes the model parameters as:
\[\theta = \theta_{\text{frozen}} \cup \theta_{\text{adapt}}\]where:
- $\theta_{\text{frozen}}$ remains unchanged during training
- $\theta_{\text{adapt}}$ is a small, trainable subset
The optimization objective becomes:
\[\min_{\theta_{\text{adapt}}} \mathcal{L}\big(f(x; \theta_{\text{frozen}}, \theta_{\text{adapt}}), y\big)\]This formulation restricts learning to a low-dimensional subspace of the full parameter space.
Adapter-Based Fine Tuning
Architectural Placement
Adapters are lightweight neural modules inserted within transformer layers, typically after the attention block or feedforward network.
Mathematical Formulation
Given a hidden representation $h \in \mathbb{R}^d$, an adapter computes:
\[h_{\text{adapter}} = h + W_{\text{up}} \, \sigma(W_{\text{down}} h)\]where:
- $W_{\text{down}} \in \mathbb{R}^{r \times d}$
- $W_{\text{up}} \in \mathbb{R}^{d \times r}$
- $r \ll d$
Only $W_{\text{down}}$ and $W_{\text{up}}$ are trainable.
Characteristics
- Preserves the original network depth
- Enables task-specific modularity
- Introduces minor inference latency due to additional layers
Adapters are particularly useful in multi-task and continual learning settings.
Low-Rank Adaptation (LoRA)
Motivation
Transformer layers rely heavily on large linear projections. Updating these matrices directly is inefficient. LoRA constrains updates to a low-rank subspace.
Mathematical Decomposition
For a weight matrix $W \in \mathbb{R}^{d \times d}$, the adapted weight is:
\[W' = W + \Delta W\]where:
\[\Delta W = B A\]with:
- $A \in \mathbb{R}^{r \times d}$
- $B \in \mathbb{R}^{d \times r}$
- $r \ll d$
Only $A$ and $B$ are trainable.
Application in Transformers
LoRA is typically applied to attention projections:
- Query: $Q = X W_Q + X B_Q A_Q$
- Key: $K = X W_K$
- Value: $V = X W_V$
The attention operation becomes:
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{Q K^\top}{\sqrt{d_k}}\right) V\]where $Q$ includes the low-rank adaptation.
Practical Properties
- No inference overhead after merging weights
- Compatible with mixed-precision training
- Multiple LoRA adapters can coexist on a single backbone
Prompt and Prefix Tuning
Prompt Tuning
Prompt tuning optimizes a set of learnable embeddings prepended to the input sequence:
\[X' = [P_1, P_2, \dots, P_k, X]\]Only the prompt parameters $P$ are trained.
Prefix Tuning
Prefix tuning injects learned key-value pairs into each transformer layer:
\[K' = [K_{\text{prefix}}; K], \quad V' = [V_{\text{prefix}}; V]\]This modifies attention distributions without changing token embeddings.
Bias and Normalization Fine Tuning
An extreme PEFT variant trains only:
- Bias parameters
- LayerNorm scale and shift parameters
Despite minimal parameter updates, this approach can significantly alter activation statistics across layers.
Theoretical Perspective
PEFT methods exploit two key properties of large neural networks:
- Redundancy in over-parameterized models
- Local linearity of the loss landscape near pre-trained optima
By constraining optimization to a low-dimensional manifold, PEFT enables efficient task adaptation without disrupting global representations.
Comparison of PEFT Methods
| Method | Trainable Params | Expressiveness | Inference Overhead |
|---|---|---|---|
| Adapters | Low | High | Low |
| LoRA | Very Low | High | None |
| Prefix Tuning | Extremely Low | Medium | None |
| Bias Only | Minimal | Low | None |
Practical Considerations
PEFT is particularly effective when:
- Model size exceeds available training memory
- Multiple downstream tasks share a single backbone
- Fast iteration and deployment flexibility are required
In production systems, PEFT simplifies versioning by decoupling base models from task-specific adaptations.
Conclusion
Parameter Efficient Fine Tuning enables scalable adaptation of large models by restricting learning to a structured subset of parameters. As model sizes continue to increase, PEFT techniques are becoming foundational to practical large-scale machine learning systems.
References
- Houlsby et al., Parameter-Efficient Transfer Learning for NLP, ICML 2019
- Hu et al., LoRA: Low-Rank Adaptation of Large Language Models, ICLR 2021
- Li & Liang, Prefix-Tuning, ACL 2021
- Lester et al., Prompt Tuning, EMNLP 2021
- Zaken et al., BitFit, ACL 2022
- Dettmers et al., QLoRA, NeurIPS 2023