Self Attention Mechanism - Learning Contextualized Embeddings
- 10 minsAttention mechanism allows a neural network to assign a different amount of weight or attention to each element of a sequence, e.g., for a test sequence, the elements are tokens.
The term self in self-attention mechanism implies that we are computing the attention weights for all the hidden states using the same sequence. This is different from the attention mechanism in the Recurrent Neural Net [2] setup, as the relevance of each encoder hidden state to the decoder hidden state depends on the timestamp of the decoder sequence.
This infamous technique was introduced in the research paper [1], published in 2017 by Ashish Vaswani et al.
Main Idea
Self-attention allows us to weight our token (word) embeddings so that we can modify them based on the context in which they are used. For example:
Sentence 1 : The monitor in be office is not working properly. Sentence 2 : Vaibhav needs to monitor his diabetes closely.
In both examples, the word monitor is used in different contexts. In sentence 1, it is used as a noun, while in sentence 2, it is used as a verb. What the self-attention mechanism does is modify the embeddings based on the context in which the token has appeared.
The embeddings of monitor in the first sentence would be more tuned towards office supplies and computer accessories, while the same token embedding for the second sentence would be more tuned towards quantification and observation.
Methodology
We tune the embeddings of the token based on the weighted average of the embedding of the neighboring tokens in the given context. Let the embeddings of an $n$ token sequence be -
\[(x_1, x_2, x_3, ..., x_n)\]The self attention mechanism changes the embeddings to -
\[(x_1^{'}, x_2^{'}, x_3^{'}, ..., x_n^{'})\]Using the following relationship -
\[x_i^{'} = \Sigma_{j = 1}^n w_{ij}x_j\]Where $w_{ji}$ are the attention weights and are normalized such that -
\[\Sigma_{j = 1}^nw_{ij} = 1\]In matrix notation -
\[x_i^{'} = W_{i}X\]Where -
\[\begin{align*} W_{i} = \left[ \begin{array}{ccccc} w_{i1}\ w_{i2}\ . . w_{in}\\ \end{array} \right]_{1 \times n} \ \ \ X = \left[\begin{array}{cccc} - - x_1 - - \\ - - x_2 - - \\ . . . . \\ . . . . \\ - - x_n - -\\ \end{array} \right]_{n\times d} \end{align*}\]Embeddings generated by this method are called contextualized embeddings.
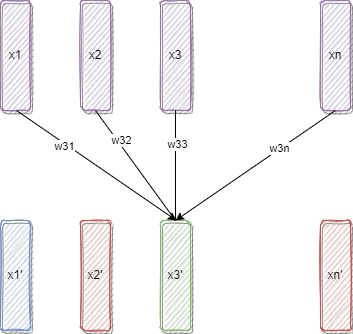
Attending to input tokens using the weighted average
These attention weights, $w_{ij}$ are calculated during the training process. One of the ways we calculate the attention scores are using the Scaled dot product method.
Scaled Dot Product Attention
1. Creating Query, Key and Value Matrices
Project all the token embeddings to into three vectors -
- Query
- Key
- Value
E.g. when projecting the token embeddings to query vectors we use an embeddings layer. Let-
- $d$ - Embedding dimension of the input token
- $d_q$ - Embedding dimension of the query vector. Then a single token is represented as -
And the weights of the embedding layers are -
\[\begin{equation*} W_q = \left[\begin{array}{ccc} wq_{11}\ wq_{12}\ ...\ wq_{1d_k} \\ wq_{21}\ wq_{22}\ ...\ wq_{2d_k} \\ . . . \\ . . . \\ wq_{d1}\ wq_{d2}\ ...\ wq_{dd_k} \\ \end{array} \right]_{d \times d_q} \end{equation*}\]The query vectors are -
\[q_i = x_iW_q\]Similarly, the embedding weights for key and value vectors are $W_k$ and $W_v$ with the dimensions being $d_k$ and $d_v$, and the following embedding vectors are calculated as -
\[\begin{align*} k & = x_iW_k \\ v & = x_iW_v \end{align*}\]$\therefore$ The matrices $Q$ (query), $K$ (key) and $V$ (value) are calculated as follows -
\[\begin{align*} Q_{n \times d_q} & = X_{n \times d}W_{q\ d \times d_q} \\ K_{n \times d_k} & = X_{n \times d}W_{k\ d \times d_k} \\ V_{n \times d_v} & = X_{n \times d}W_{v\ d \times d_v} \\ \end{align*}\]For calculating the attention scores for self attention mechanism, we need to set $d_k = d_q = d_a$, as we’ll see in the next step.
2. Calculating Similarity Scores between Queries and Keys
Compute the attention scores by determining how much the query and key vectors relate to each other. This is done by a similarity function, and as the name suggests, we use the dot product as our similarity metric; hence, the dimensions of the key and value pairs must be the same.
The query and key matrices for a sequence of $n$ tokens are given as follows -
\[\begin{align*} Q = \left[\begin{array}{ccccc} - - q_1 - - \\ - - q_2 - - \\ .... \\ - - q_n - - \\ \end{array}\right]_{n \times d_a} W = \left[\begin{array}{ccccc} - - k_1 - - \\ - - k_2 - - \\ .... \\ - - k_n - - \\ \end{array}\right]_{n \times d_a} \\ \\ S = \left[\begin{array}{cccc} s_{11}\ s_{12}\ ... s_{1n} \\ s_{21}\ s_{22}\ ... s_{2n} \\ .... \\ s_{n1}\ s_{n2}\ ... s_{nn} \\ \end{array}\right]_{n \times n} = QK^T \end{align*}\]Where -
\[s_{ij} = \Sigma_{l =1}^{d_a} q_{jl}k_{il}\]This $s_{ij}$ is the similarity score and is interpreted as how much the query vector $q_i$ is similar to the key vector $k_j$.
3. Calculating the Normalized Attention weights
Calculate the attention weights.The Attention scores $S$ are normalized, and a softmax is taken across the rows so that the column value sum is 1 i.e. $\Sigma_{j = 1}^{n}w_{j,i} = 1$. The scaled dot product attention weights are calculated as follows -
\[\begin{align*} s_{ij}' & = \frac{s_{ij}}{\sqrt{d_a}} \\ w_{ij} & = \frac{e^{s_{ij}'}}{\Sigma_{j = 1}^{n}e^{s_{ij}'}} \\ \\ & \Sigma_{j = 1}^ nw_{ij} = 1 \end{align*}\]$\therefore$ The attention weights $W$ is given by -
\[\begin{align*}W & = \left[\begin{array}{cccc} w_{11}\ w_{12}\ ... w_{1n} \\ w_{21}\ w_{22}\ ... w_{2n} \\ .... \\ w_{n1}\ w_{n2}\ ... w_{nn} \\ \end{array}\right]_{n \times n} = softmax(\frac{QK^T}{\sqrt{d_a}}) \end{align*}\]This $w_{ij}$ is the attention weight and is interpreted as how much the query vector $q_i$ is similar to the key vector $k_i$.
4. Learning Contextualized Embeddings Using the attention weights
Now that our weight vector is calculated, we take the linear combination of the value vectors with attention weights as the coefficients. Given an input value vector $x_i^v$ and its corresponding attention weight vector $W_{.i}$, which is the $i^{th}$ column of the attention weight matrix $W$, we update the representation of the tokens as the weighted average of the neighboring tokens as follows -
\[x_i' = \Sigma_{j = 1}^{n}w_{ij}v_j\]The final representation is as follows -
\[\begin{align*} X'_{n \times d_v} & = W_{n \times n}*V_{n \times d_v} = softmax(\frac{QK^T}{\sqrt{d_k}})V \end{align*}\] \[\begin{align*} X'_{n \times d_v} = \left[\begin{array}{cccc} - - x'_1 - - \\ - - x'_2 - - \\ . . . \\ . . . \\ - - x'_d - - \\ \end{array} \right]_{n \times d_v} = \left[\begin{array}{ccc} w_{11}\ w_{12}\ ...\ w_{1n} \\ w_{21}\ w_{22}\ ...\ w_{2n} \\ . . . \\ . . . \\ w_{n1}\ w_{n2}\ ...\ w_{nn} \\ \end{array} \right]_{n \times n} \times \left[\begin{array}{ccc} v_{11}\ v_{12}\ ...\ v_{1d_v} \\ v_{21}\ v_{22}\ ...\ v_{2d_v} \\ . . . \\ . . . \\ v_{n1}\ v_{n2}\ ...\ a_{vd_v} \\ \end{array} \right]_{n \times d_v} \end{align*}\]If, for instance, the value $w_{12}$ (i.e., query 1 is most similar to key 2) is high, the value of $x’_1$ is more influenced by the vector $v_2$.
The calculation of attention weights using the self-attention mechanism can be summarized in the following figure - 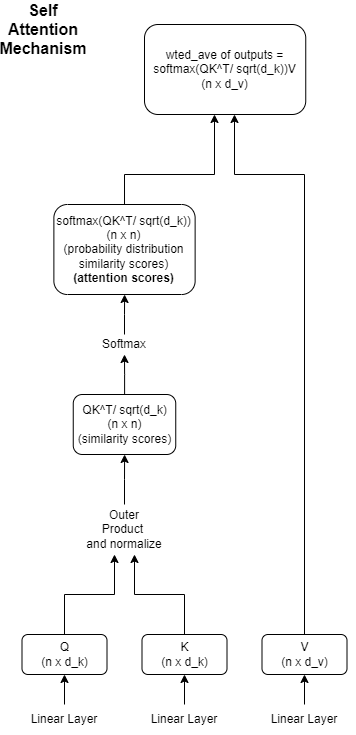
Self Attention Mechanism
Interpretation of query, key and value
The attention process can indeed be likened to a retrieval process, and the terminology of query, key, and value is directly related to retrieval systems. For example, let’s imagine using the Amazon shopping website as an analogy: when you search for a product (query), the query is matched to keys such as product title, category, and so on, associated with each candidate product available in Amazon’s database. The best-matched products (values) are then presented to you.
As we’ve previously discussed, $w_{ij} \in W$ represents the similarity value between the query $i$ ($q_i$) and the key $j$ ($k_j$). The values of $w_{ji}$ are normalized and scaled so that the sum $\sum_{j = 1}^n w_{ij} = 1$. In other words, for a given query, the set of all similarity values for all the keys forms a probability distribution.
When $w_i$ is set to be a one-hot vector with the $j^{th}$ value set to one, we obtain a single retrieved vector ($v_2$) as the output for the $i^{th}$ row of $X’$. The self-attention mechanism relaxes this constraint because $w_i$ is a smooth probability distribution of similarity values over the keys (videos) for a given query. This results in an equivalent to a ranked recommendation of videos from the database for a given query.
Multi-Head Attention -
In the previous section, we calculated the scaled dot product attention using a single set of query, keys, and values. However, in practice, multiple sets of these parameters are preferred, with each set creating its own attention head. The primary reason for this architectural choice is that each attention head has its own set of weights and can focus on a different aspect of similarity.
For each set of (Q, K, V), a self-attention routine is performed independently by each attention head. The self-attention outputs from each head are then concatenated into a single vector, and this concatenated vector is typically projected to a smaller or larger vector dimension using a linear layer.
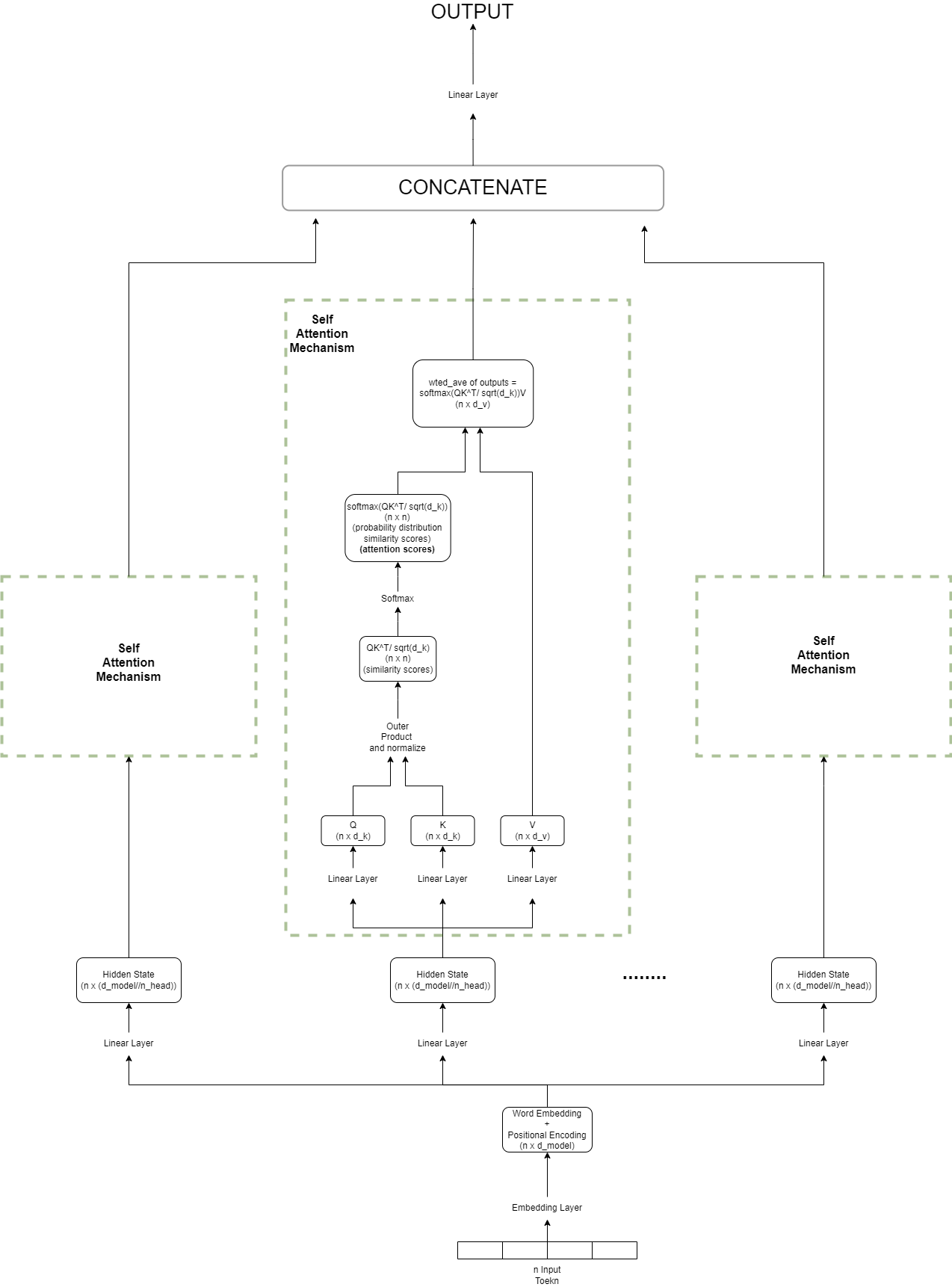
Multihead Attention Mechanism
Interpretation of Multi-Head Attention mechanism
While a single self-attention mechanism calculates the similarity scores between the query and key values, we may need multiple such mechanisms (heads) to capture various aspects of similarity scores.
Let’s revisit our video recommendation system scenario. Suppose we have rich information about video titles, including details like the creator, topic, demographic it is popular in, etc., and all this information is embedded in our vector representations. Now, when we query a video title to find similar videos, the multi-head attention mechanism will consider video similarity across multiple dimensions. As a result, it will recommend video titles that are not only similar in content but also viewed by a similar demographic and created by similar creators. This multi-dimensional approach enhances the recommendation system’s ability to provide more relevant and personalized video suggestions.
Hence, we see how the self-attention mechanism, used in conjunction with transformer models [1], is an important tool that assists us in various use cases [2][3] such as machine reading, abstractive summarization, or image description generation.
References -
1. Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, & Illia Polosukhin. (2023). Attention Is All You Need.
2. Minh-Thang Luong, Hieu Pham, & Christopher D. Manning (2015). Effective Approaches to Attention-based Neural Machine Translation_. CoRR, abs/1508.04025._
3. Liu, Y.T., Li, Y.J., Yang, F.E., Chen, S.F., & Wang, Y.C. (2019). Learning Hierarchical Self-Attention for Video Summarization. In 2019 IEEE International Conference on Image Processing (ICIP) (pp. 3377-3381).
4. R. Sharma, S. Palaskar, A. W. Black and F. Metze, “End-to-End Speech Summarization Using Restricted Self-Attention,” ICASSP 2022 - 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, Singapore, 2022, pp. 8072-8076, doi: 10.1109/ICASSP43922.2022.9747320.